
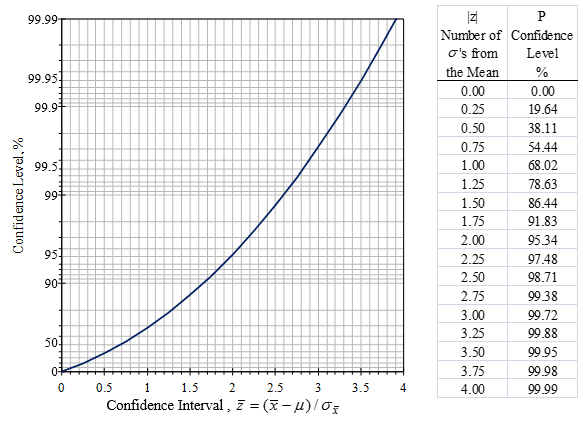
$\Overline$ = 78 pages Confidence level = 90% Standard deviation = 8 First we need to find the Z value of 95% confidence level from the following table.Example: A 95% Confidence Interval for Movie Run TimeĪ 95% confidence interval for the mean runtime of Netflix movies is (98, 111).
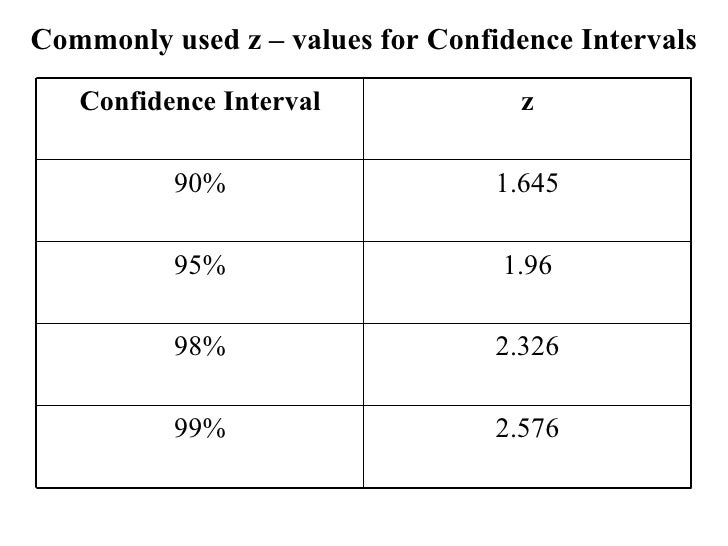
In some cases, they will be given in the problem, however, if they are not mentioned, you can calculate these values yourself. While solving the problems related to the confidence interval, you should follow the following steps: Step 1Ĭalculate the mean and standard deviation of the population. Steps for Calculating the Confidence Interval In statistics, the 689599.7 rule, also known as the empirical rule, is a shorthand used to remember the percentage of values that lie within an interval. In the next section, we will discuss the steps to find the confidence interval. Margin of error =Critical value of the statistic x standard deviation If you only have the percentile, Z scores are commonly. In other words, a 95 confidence interval comprises all values above the 2.5th percentile and below the 97.5th percentile (1-0.025 0.975). Therefore, the alpha value has to be split between both sides: 0.05/2 0.025 0.05/2 0.025. The formula for computing the margin of error is given below: But in our case, the confidence interval is two-sided. For instance, a confidence interval of 98% with a 5% margin of error means that your value will be within 5 percentage points of the real value of the population 98% of the time. Margin of ErrorĪ margin of error reflects by how much percentage points your result will deviate from the real value of the population. You are 95% confident that the result of this survey is accurate. What does this interval reflect? Well, it means that the residents of that locality spend between \$500 to \$800 on groceries per month. Thus, the confidence interval at 98 confidence level is 3.18 to 3.42. is-the-z-score-for-a-98-confidence-interval Confidence Interval Calculator Using. After testing the statistics at a 95% confidence level, you get a confidence interval of (500,800). 98 percent confidence nterval t score questions Confidence Interval. The confidence limits represent the two extreme values of the confidence interval that also reflect the range.įor instance, a survey is conducted in a locality to determine how much its residents spend on the grocery every month. It means that if you conduct the survey repeatedly, then 98% of the time the results of the poll will match the existing results.Ĭonfidence intervals are represented in the form of numbers and they reflect the results of the survey. Confidence levels are represented as a percentage, for instance, the confidence level of this poll is 98%. The two terms confidence intervals and confidence levels seem alike, however, there is a difference between these two terms. Confidence Intervals Vs Confidence Levels We can calculate a critical value z for any given confidence level using normal distribution calculations. More precisely, it's actually 1.96 standard errors. Confidence intervals are associated with confidence levels. If we want to be 95 confident, we need to build a confidence interval that extends about 2 standard errors above and below our estimate. For example, the area between z1.28 and z-1.28 is approximately 0.80. The area between each z value and the negative of that z value is the confidence percentage (approximately). Note that these values are taken from the standard normal (Z-) distribution. The confidence interval helps you to determine how confident you can be that the results from a survey reflect the opinion or trend of the entire population. The above table shows values of z for the given confidence levels. These intervals are mostly accompanied by the margin of error. For example, if the sample size is 15, then df14, we can calculate the t-score for the lower and upper tails of the 95 confidence interval in R: > qt (0.025,14) 1 -2.144787. A confidence interval reflects the extent of the uncertainty of a specific statistic. For example, to generate t values for calculating a 95 confidence interval, use the function qt (1-tail area,df).


 0 kommentar(er)
0 kommentar(er)
